Was uns die Natur über Heilige Geometrie lehren kann

Eines der grossartigsten Geschenke, das die menschliche Seele vom Schöpfer erhalten hat ist die Fähigkeit, sich an der unübertrefflichen Vielfalt und beglückenden Schönheit der Natur zu erfreuen, und eine der angeborenen Eigenschaften des menschlichen Geistes ist es in den äusseren Erscheinungen der Welt und im Aufbau der Schöpfung nach Gesetzmässigkeiten und Verwandtschaften zu forschen. Dieser Beitrag soll zeigen, in welch erfüllender Weise sich diese beiden Aspekte des Menschseins verbinden lassen und welche Rolle die Heilige Geometrie dabei spielen kann.

Wenn man die in der Natur vorkommenden Formen und Wachstumsprinzipien untersucht dann fällt auf, in wie ungewöhnlich vielen Fällen die Zahlen der Fibonacci-Folge und das Verhältnis des Goldenen Schnittes erscheinen. Es ist faszinierend festzustellen, welch überragende Rolle die Fibonacci-Zahlen beim Wachstum von Pflanzen und bei der natürlichen Formenbildung spielen und wo überall in der Natur das Verhältnis des Goldenen Schnittes beobachtet werden kann. Am Ende dieses Beitrags werde ich auf die rein zahlenmässigen Aspekte dieser zwei eng miteinander zusammenhängenden mathematischen Begriffe kurz eingehen.

Bei der genaueren Betrachtung der äusseren Strukturen und Formen in der Natur werden wir immer wieder daran erinnert, dass hinter allen schöpferischen Kräften die gleiche spiralig-wirbelnde, aufbauende und formende Intelligenz und Energie steckt. Ob es sich nun um Sonnenblumen, Tannenzapfen, Whirlpools, Tierproportionen, unsere DNS oder Spiralgalaxien handelt, vom unendlich Kleinen bis zum unendlich Grossen, immer sind es die gleichen Grundprinzipien, die das Wachstum, den Aufbau und den Ablauf der Dinge bestimmen.

Man kann Zahlenmuster und geometrische Grundformen entdecken, die offenbar der gesamten geschaffenen Welt zugrunde liegen. Und so ist die Heilige Geometrie der einzigartige Ort, wo sich Naturwissenschaft und Spiritualität treffen – und schon immer getroffen haben, seit der menschliche Geist sich darum bemüht hat, die Grundmuster und organisierenden Kräfte zu erkennen, die den Aufbau und die äusseren Erscheinungsformen der belebten und (scheinbar) unbelebten Materie bestimmen.

Es ist absolut verblüffend zu entdecken, wie verbreitet und breit gefächert die den Goldenen Schnitt charakterisierende Zahl  Phi = 1.61803…  in der Natur vorkommt. Es gibt keine Zahl, die in der Schöpfung eine so ausgezeichnete Rolle spielt wie die Zahl Phi.

Und es gibt keine Zahlreihe, die in der Natur so häufig beobachtet werden kann, wie die Fibonacci-Folge, die auch als das Akkumulationsgesetz der Natur verstanden werden kann. Die Fibonacci-Zahlenfolge beschreibt, wie die Dinge wachsen, sich ausbilden und sich vervielfachen auf der Basis des jeweils bereits Bestehenden.

Es verwundert auch nicht, dass diese Erkenntnisse in den alten Kulturen auf der ganzen Welt in den Mysterienschulen gelehrt wurden und dass das Wissen dazu verwendet wurde, um Tempel, Kirchen und heilige Stätten zu bauen. Die Menschen unseres heutigen Zeitalters haben schon früh begonnen, diese alten Strukturen und Plätze zu studieren und die moderne Wissenschaft beginnt langsam zu verstehen, welches die Bedeutung und der Zweck ist hinter diesen Werken, und welche Kenntnisse die alten, in die Geheimnisse der Schöpfung eingeweihten Schöpfer und Erbauer dieser Strukturen hatten.

Es soll hier nicht vertieft auf mathematische Details eingegangen werden, man kann die im Folgenden gezeigten, wunderschönen Aufnahmen aus der Natur einfach auf sich wirken lassen. Für jene Leser, die sich auch dem geometrisch-theoretischen Aspekt zuwenden möchten, werden am Schluss und sozusagen als intellektuelle Anregung ein paar Bilder gezeigt, bei denen einige Linien eingezeichnet sind, die auf die zugrundeliegende, geometrische Struktur hinweisen. Wer an den Themen rund um die Heilige Geometrie stärker interessiert ist, findet dazu reichhaltiges Material in Büchern und in Artikeln im Internet.

Anhang: Zur Mathematik der Fibonacci-Folge und des Goldenen Schnittes

A) Die Fibonnacci-Folge erhielt ihren Namen vom italienischen Mathematiker Leonardo von Pisa (1170 – 1250), genannt Fibonacci. In seinem Buch Liber abaci findet sich im 12. Kapitel folgende Aufgabe:

„Ein Mann hält ein Kaninchenpaar an einem Ort, der gänzlich von einer Mauer umgeben ist. Wir wollen nun wissen, wie viele Paare von ihnen in einem Jahr gezüchtet werden können, wenn die Natur es so eingerichtet hat, dass diese Kaninchen jeden Monat ein weiteres Paar zur Welt bringen und damit im zweiten Monat nach ihrer Geburt beginnen.“

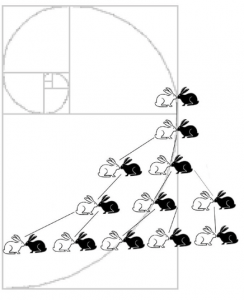
Anzahl der neugeborenen Kaninchen gemäss der Finbonacci-Aufgabe. Die Anzahl der Kaninchenpaare findet man auch als die Anzahl der Vierecke in der aus lauter Quadraten aufgebauten Rechteckfigur, die wiederum im Zusammenhang steht mit dem Goldenen Schnitt.

Wenn man sich bemüht, diese Frage zu beantworten, kommt man auf folgende Zahlenfolge:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …    für die Anzahl der neugeborenen Kaninchenpaare nach einem, zwei, drei, … Monaten.

Wie man sofort erkennt kann man diese Zahlenfolge leicht beliebig weiter fortsetzen, denn sie hat ein sehr einfaches Bildungsgesetz. Welches?

Man kann leicht bestätigen: Jede Zahl dieser Folge entsteht, indem man die beiden vorhergehenden Zahlen addiert.

Im 7. Monat kommen 13 Paare zur Welt, diese Zahl ergibt sich als Summe der beiden vorangehenden Zahlen: 5 + 8 = 13;
Im 12. Monat kommen144 Kaninchenpaare zur Welt; es ist 55 + 89 = 144 ; usw.

Es mag für Viele bestimmt reizvoll sein, in den oben gezeigten Bildern diese Zahlen zu suchen (als Hinweis möge zum Beispiel das Stichwort ‚Anzahl Spiralen’ dienen) – wobei natürlich nicht in allen Bildern diese Zahlen offensichtlich erscheinen.

B) Der Goldene Schnitt

Man spricht von der Stetigen Teilung oder vom Goldenen Schnitt, wenn eine Strecke a so geteilt wird, dass das Verhältnis der Stecke a zur grösseren Teilstrecke x gleich gross ist wie das Verhältnis von x zu kleineren Teilstrecke  y = a – x:

a : x = x : (a – x)

Mit etwas Mathematik findet man, dass dieses Verhältnis den Wert hat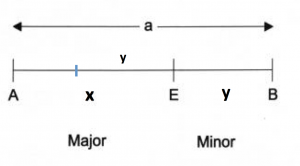

a : x = (1 + √ 5 ) / 2 = 1.61803…

Diese Zahl nennt man auch Phi (im Unterschied zur Kreiszahl Pi = 3.14…).

Es ist also Phi = 1.61803… (eine so genannte irrationale Zahl, die nicht als Verhältnis von zwei ganzen Zahlen geschrieben werden kann).

Die grosse Teilstrecke wird Major M genannt, die kleinere Teilstrecke heisst Minor m.

Diese Art Teilung heisst ‚Stetige Teilung’, weil wenn man jetzt y in der grösseren Strecke x abträgt, dann wird x durch y wieder im gleichen Verhältnis geteilt. Das heisst es ist

x : y = y : (x – y) = Phi

In der gleichen Weise kann man fortfahren: wenn immer man die neue kleinere Teilstrecke in der unmittelbar grösseren abträgt, wird diese wieder im Verhältnis Phi geteilt. Auch in der umgekehrten Richtung funktioniert es: verlängert man die gegeben Strecke a um die Strecke x, dann wird die neue Strecke a + x durch a im Verhältnis des Goldenen Schnittes geteilt:

(a + x) : a = a : x = Phi.

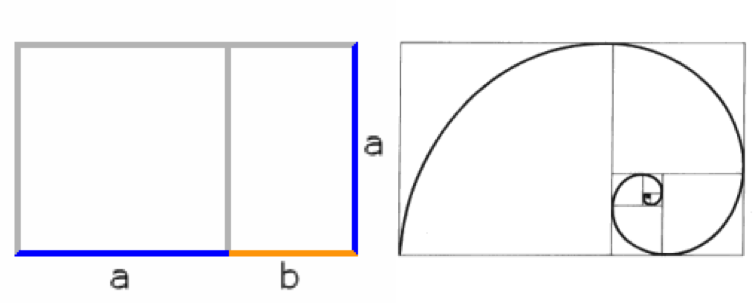Bildet man aus den Strecken x und y ein Rechteck, dann erhält man ein so genanntes ‚Goldenes Rechteck’, das man mit dem gleichen Verfahren in kleinere Goldene Rechtecke aufteilen kann oder zu grösseren Goldenen Rechtecken erweitern kann.

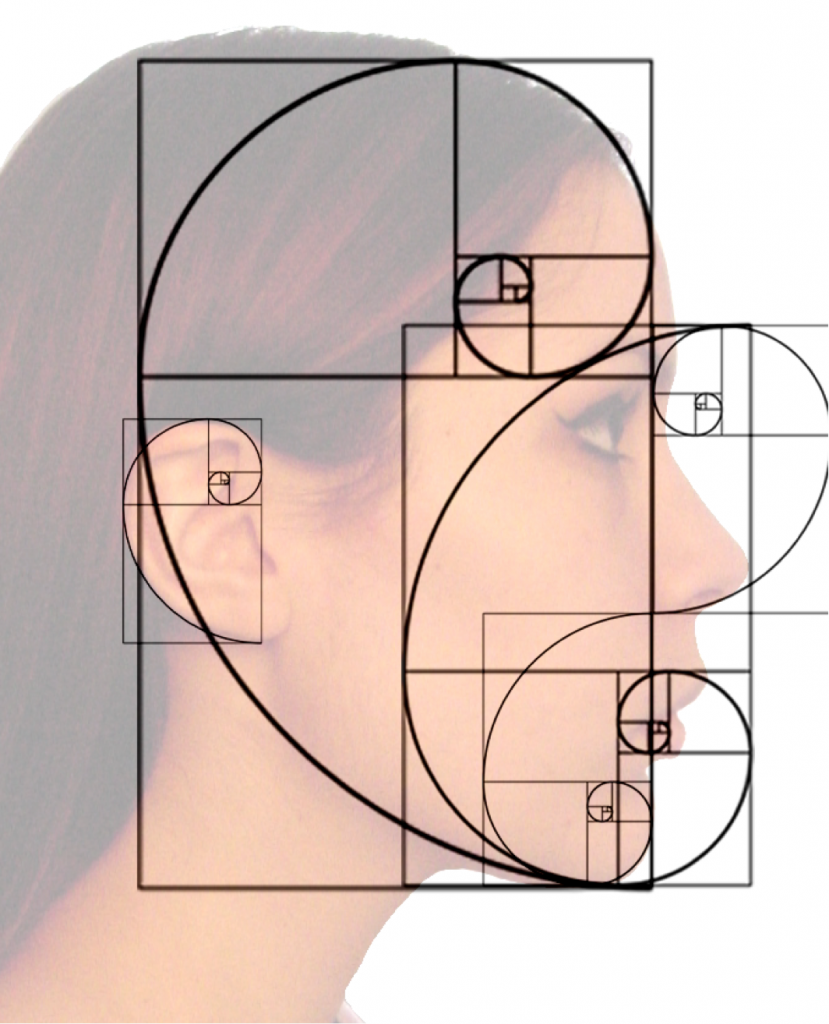
Durch Einzeichnen der Viertelbögen erhält man eine ‚Goldene Spirale’, die man häufig in der Natur findet.

Und welches ist nun der Zusammenhang zwischen den Fibonacci-Zahlen und dem Goldenen Schnitt?

Wenn man von der Fibonacci-Folge zwei aufeinanderfolgende Zahlen nimmt und die grössere Zahl durch die vorangehende Zahl teilt, dann erhält man einen Wert, der umso genauer bei der Zahl Phi liegt, je weiter man in der Fibonacci-Folge voranschreitet:

89 : 55 = 1.61818 ,   144 : 89 = 1.61798 ,   233 : 144 = 1.61806 ,   377 : 233 = 1.61803 (dieser Wert stimmt, auf 5 Stellen nach dem Komma gerundet, bereits mit der Zahl Phi überein).

Entsprechend erhält man, wenn man Rechtecke mit den Fibonacci-Zahlen bildet, annähernd Goldene Rec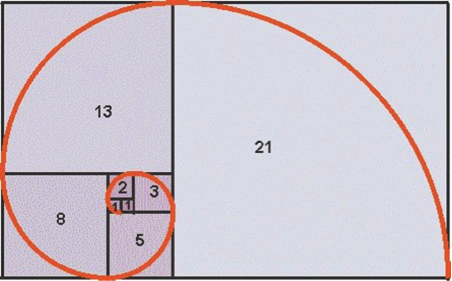htecke mit den darin enthaltenen (annähernden) Goldenen Spirale:

Goldene Rechtecke und der Goldene Schnitt kommen auch in der Kunst ausserordentlich häufig vor. Sehr oft haben Künstler diese geometrischen Proportionen verwendet, ohne sich dessen bewusst zu sein, einfach weil sie die Werke, die sie in mit den entsprechenden Proportionen geschaffen haben als besonders harmonisch empfunden haben. Im Internet findet man zu diesem Thema überaus viele überraschende und erhellende Beispiele.

Das Feld für eigene Forschungen auf diesem Gebiet, aber auch für eigene, kreative, künstlerische Schöpfungen mit diesen von der Natur bevorzugten Zahlen und Proportionen ist weit offen und kann von jedermann ohne tiefe Vorkenntnisse genutzt werden!

Quellen: Die Fotographien stammen aus dem Internet und teilweise dem Artikel   “15 Plants That Teach Us Sacred Geometry”